⬅️199. Binary Tree Right Side View

Medium | Grind 75 | January 8th Sunday, 2023

Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Constraints:

• The number of nodes in the tree is in the range [0, 100].

• -100 <= Node.val <= 100

Example 1

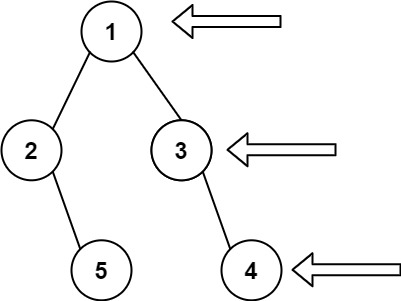
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]

Example 2

Input: root = [1,null,3]
Output: [1,3]

Example 3

Input: root = []
Output: []

SOLUTION

The right-side view of a tree consists of the nodes that can be seen when the tree is viewed from the right side. To find this view, we will use a queue to traverse the tree level by level, starting at the root. The queue will store the nodes and their corresponding levels. If the current node's level is greater than or equal to the size of the result list, which stores the nodes in the right-side view, it means that we have already processed the rightmost node at that level. If the current node's level is higher than the size of the result list, we will add the current node to the result list. To ensure that we always consider the rightmost node of each level, we will add right child of the current node to the queue before the left child.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        # store the right side view 
        result = [] 

        # queue to iterate the tree level wise
        # contains the node and its level
        queue = deque() 

        if root: 
            # node: root and level: 1
            queue.append((root, 1))
        
            while queue: 
                node, level = queue.popleft()

                # first node of that level
                if level > len(result): 
                    result.append(node.val)
                
                # always append the right node first because right side view
                if node.right: 
                    queue.append((node.right, level+1))
            
                if node.left: 
                    queue.append((node.left, level+1))

        return result

TIME AND SPACE COMPLEXITY

TIME: O(n), where n is the number of nodes in the tree. This is because the code processes each node of the tree once.

SPAC: O(n), because the queue used to store the nodes during the breadth-first search can store up to n nodes at a time in the worst case when the tree is a complete binary tree (i.e., each level is fully filled except possibly the last level, and all nodes are as far left as possible). In the worst case, when the tree is a complete binary tree, the space complexity is O(n). In the best case, when the tree is a straight line, the space complexity is O(1).

* Written with help from ChatGPT *