🔟542. 01 Matrix

Medium | Grind 75 | January 5th Thursday, 2023

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 10^4

• 1 <= m * n <= 10^4

• mat[i][j] is either 0 or 1.

• There is at least one 0 in mat.

Example 1

Example 1:

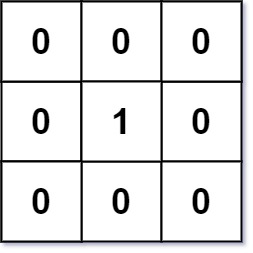
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2

Example 2:

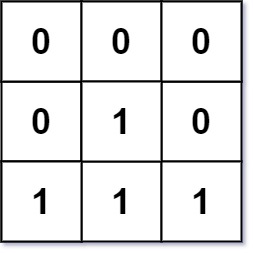
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

SOLUTION

To solve this problem, we can use a breadth-first search approach. We start from each position in the matrix that has a value of 0 since the distance from a 0 to itself is 0. We can then explore the neighbors of each 0 and update their distances to 1 since they are the immediate neighbors of the 0. Any non-zero neighbor of a 0 has a distance of 1 because it is immediately adjacent to a 0.

As we explore the neighbors of each 0, we add them to a queue so that we can process their own neighbors in the next iteration. When we later process these indices, we update the distances of their unprocessed neighbors by adding 1 to the distance of the current element. This is because the unprocessed neighbors are immediately adjacent to the current element, and their distance is therefore 1 more than the distance of the current element, which is the minimum distance to a 0.

We continue this process until we have looked at every single element in the matrix. By the end of the search, we will have determined the shortest distance from each element to its nearest 0.

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        """
            1. locate all the zeros & store in a queue. We know at this location, the distance is zero. 
            2. any non-zero neighbor of zero has distance 1.
            3. store the index of the non-zero neighbors in the queue. 
            4. pop and check the neighbors for every element in the queue until it is empty. 
        """

        ROWS = len(mat)
        COLS = len(mat[0])

        # coordinates of four neigbors: RIGHT, DOWN, LEFT, UP
        neighbors = [(0,1), (1,0), (0,-1), (-1,0)]

        # initialize result mat with 0s 
        result = [[0 for i in range(COLS)] for j in range (ROWS)]

        #queue to store elements we need to process
        queue = deque()

        # locate all the zeros in mat
        for i in range(ROWS): 
            for j in range(COLS): 
                if mat[i][j] == 0: 
                    # 0 because distance is 0
                    queue.append((i, j, 0))
                    mat[i][j] = '#'

        # process every element
        while queue: 
            row, col, distance = queue.popleft() 
            result[row][col] = distance
            mat[row][col] = '#'

            for neigh in neighbors: 
                new_col, new_row = col + neigh[1], row + neigh[0]
                if 0 <= new_col < COLS and 0 <= new_row < ROWS and mat[new_row][new_col] != '#': 
                    queue.append((new_row, new_col, distance+1))
                    mat[new_row][new_col] = '#'
            
    
        return result

TIME AND SPACE COMPLEXITY

TIME: O(n) , where n is the total number of elements in the matrix (rows x columns). This is because we iterate over every element in the matrix once. In the worst case, where every element in the matrix is a 0, we have to iterate over the matrix (n elements) once and the queue (also of size n) again, resulting in a time complexity of O(2n).

SPACE: O(n), where n is the total number of elements in the matrix. Similar to the time complexity, in the worst case with all 0s, we need O(2n) space, which includes n space for the result and n space for the queue.

* Written with help from ChatGPT *